When she is bored, Jo Coder likes to play the following game with coins on a table. She takes a set
of distinct coins and lines them up in a row. For example, let us say that she has a penny (P, worth
$0.01), a nickel (N, worth $0.05), and a dime (D, worth $0.10). She lines them up in an arbitrary
order, (for example, D N P), and then moves them around with the goal of placing them in strictly
increasing order by value, that is P N D (i.e., $0.01, $0.05, $0.10). She has particular rules that she
follows:
• The initial coin line-up defines all positions where coins can be placed. That is, no additional
positions can be added later, and even if one of the positions does not have a coin on it at
some point, the position still exists.
• The game consists of a sequence of moves and in each move Jo moves a coin from one
position to an adjacent position.
• The coins can be stacked, and in a move Jo always takes the top coin from one stack and
moves it to the top of another stack.
• In a stack of coins, Jo never places a higher-value coin on top of a lower-value coin.
For simplicity, let the coins have consecutive integer values (e.g., denote the penny as 1, nickel as
2, and dime as 3). Then, in the above example, Jo could play the game in the following way in 20
moves (where XY denotes that coin X is on top of coin Y):

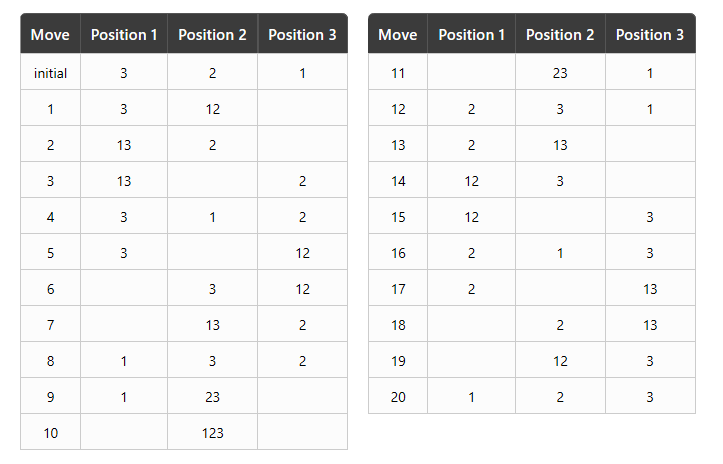
For some starting configurations, it is not always possible to obtain the goal of strictly increasing order.

The input will contain some number of test cases. A test case consists of two lines. The first line
contains a positive integer n (n < 5), which is the number of coins. We assume that the coins are
labeled 1, 2, 3, . . . n. The second line contains a list of numbers 1 to n in an arbitrary order, which
represents the initial coin configuration. For the above example, the input test case would be:
3
3 2 1
The end of test cases is indicated by 0 on a line by itself.

For each test case, output one line, which will either contain the minimal number of moves in
which Jo can achieve the goal coin line-up, or, if it is not possible to achieve the goal coin line-up,
IMPOSSIBLE.

CCC 图论 广度优先