Problem U: CCC17J5 Nailed It!
Time Limit: 2 Sec Memory Limit: 256 MBSubmit: 22 Solved: 8
[Submit] [Status] [Web Board] [Creator:]
Description
Tudor is a contestant in the Canadian Carpentry Challenge (CCC). To win the CCC, Tudor must
demonstrate his skill at nailing wood together to make the longest fence possible using boards. To
accomplish this goal, he has N pieces of wood. The ith piece of wood has integer length Li.
A board is made up of exactly two pieces of wood. The length of a board made of wood with
lengths Li and Lj is Li + Lj . A fence consists of boards that are the same length. The length of
the fence is the number of boards used to make it, and the height of the fence is the length of each
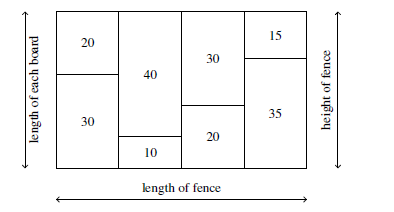
board in the fence. In the example fence below, the length of the fence is 4; the height of the fence
is 50; and, the length of each piece of wood is shown:
Tudor would like to make the longest fence possible. Please help him determine the maximum
length of any fence he could make, and the number of different heights a fence of that maximum
length could have.
demonstrate his skill at nailing wood together to make the longest fence possible using boards. To
accomplish this goal, he has N pieces of wood. The ith piece of wood has integer length Li.
A board is made up of exactly two pieces of wood. The length of a board made of wood with
lengths Li and Lj is Li + Lj . A fence consists of boards that are the same length. The length of
the fence is the number of boards used to make it, and the height of the fence is the length of each
board in the fence. In the example fence below, the length of the fence is 4; the height of the fence
is 50; and, the length of each piece of wood is shown:

Tudor would like to make the longest fence possible. Please help him determine the maximum
length of any fence he could make, and the number of different heights a fence of that maximum
length could have.
Input
The first line will contain the integer N (2 <= N <= 1 000 000).
The second line will contain N space-separated integers L1,L2,......,LN (1 <= Li <= 2 000).
For 7 of the 15 available marks, N <= 100.
For an additional 6 of the 15 available marks, N <= 1000.
For an additional 1 of the 15 available marks, N <= 100 000.
The second line will contain N space-separated integers L1,L2,......,LN (1 <= Li <= 2 000).
For 7 of the 15 available marks, N <= 100.
For an additional 6 of the 15 available marks, N <= 1000.
For an additional 1 of the 15 available marks, N <= 100 000.
Output
Output two integers on a single line separated by a single space:
the length of the longest fence
and the number of different heights a longest fence could have.
the length of the longest fence
and the number of different heights a longest fence could have.
Sample Input Copy
4
1 2 3 4
Sample Output Copy
2 1
HINT
Explanation for Sample Output 1
Tudor first combines the pieces of wood with lengths 11 and 44 to form a board of length 55.
Then he combines the pieces of wood with lengths 22 and 33 to form another board of length 55.
Finally, he combines the boards to make a fence with length 22 and height 55.
Sample Input 2
5 1 10 100 1000 2000
Sample Output 2
1 10
Explanation for Sample Output 2
Tudor can't make a fence longer than length 11, and there are 1010 ways to make a fence with length 11 by choosing any two pieces of wood to nail together.
Specifically, he may have a fence of height 1111, 101101, 10011001, 20012001, 110110, 10101010, 20102010, 11001100, 21002100 and 30003000.